19++ Area Of Non Right Angle Triangle Formula

Area Of Non Right Angle Triangle Formula. This formula works for a right triangle as well, since the since of 90 is one. Reformat the formula according to the given diagram 2.

Cm 2, m 2, mm 2 ). The area of the triangle is 88.47. Unlike the other formula for the area of a triangle, (a = \frac{1}{2}bh ), we do not need to know the vertical height.

5 4 150 lbs female bmi 50 40 apprentice nut milk brand aspirateur a cendres pour poele a pellets

Sine rule

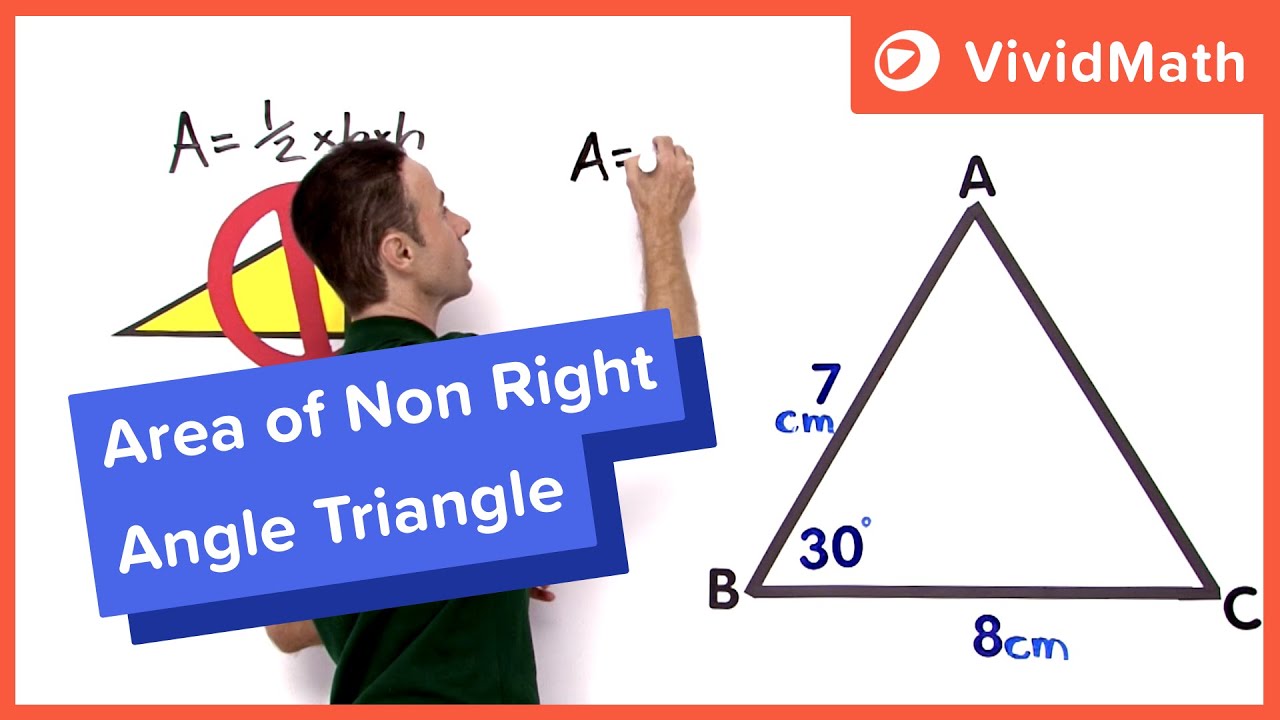
Area = ½ × (c) × (b × sin a) which can be simplified to: [area = \frac{1}{2} \times bc \times \sin a] [area = 0.5 \times 3 \times 7 \times \sin (35^\circ )] [area = 6.02255.] [area = 6.02c{m^2}(to,2,d.p.)] The area of any other triangle can be found with the formula below. Substitute in the known values 3.

Then the area of either of these triangles would be equal to that of one half of the original rectangle. Find the area of triangle abc. This formula is derived from the area of a triangle formula, a=1/2bh for any triangle abc with side a opposite a, side b opposite b and side c opposite c, height h is represented.

Now that you know the trig ratios, this formula can be changed around, using sine. Let us take a triangle abc, whose vertex angles are ∠a, ∠b, and ∠c, and sides are a,b and c, as shown in the figure below. By changing the labels on the triangle we can also get: Total area = 117 + 129.8 + 13.9.

Find the area of triangle abc. Then the area of either of these triangles would be equal to that of one half of the original rectangle. Unlike the other formula for the area of a triangle, (a = \frac{1}{2}bh ), we do not need to know the vertical height. Your final answer must be given in units 2 (e.g. We.

Substitute in the known values 3. The area of any triangle can be calculated using the formula: This formula only needs us to know two side lengths (a) and (b) and the angle between them, (c^\circ). Find the area of triangle abc. Now, if any two sides and the angle between them are given, then the formulas to calculate the.